Algebră clasa a VI-a , clasa a VII-a
Modulul unui număr reprezintă valoarea acelui număr atunci când nu luăm semnul în considerare.
Ca exemplu +3 luat în modul este egal cu 3, iar -3 luat în modul este egal tot cu 3.
Pentru modulul unui număr se mai folosește și exprimarea de valoare absolută a acelui număr.
Modulul se reprezintă prin încadrarea între două bare verticale a acelui număr.
Când avem în locul unui număr o literă, înțelegem că acea literă poate avea orice valoare, ea este necunoscuta. Dacă problema ne spune că necunoscuta x este din mulțimea numerelor întregi, modulul lui x poate avea cele două forme (așa cum am văyut în exemplul de mai sus ...odată poyitiv și o dată negativ.
Pentru scrierea celor două forme folosim exprimarea de explicitare a modulului.
Această explicitare a modulului ne ajută să putem rezolva orice problemă.
Explicitarea modulului lui x se scrie după cum urmează:
Ceea ce trebuie să reținem este că în locul lui x putem avea o expresie în care să îl avem pe x. De exemplu, rezolvarea unei ecuații cu modul:
Avem un modul egal cu 9.
Explicităm modulul și reținem că ceea ce este scris după cuvântul DACĂ este condiția în care există acea formă a modulului.
Rezolvăm inecuația de la condiția fiecărui caz și ținem cont că suntem în mulțimea numerelor întregi.
Rezolvăm ecuația care ne-a fost dată în problemă pentru fiecare caz în parte.
Soluțiile găsite sunt valabile pentru fiecare caz în parte. Scriem la final soluția ecuației.ca reuniune a celor două soluții -7 și 2.

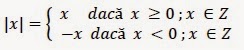

Si asta|√2-2|=
RăspundețiȘtergere2=√4 deci |√2-√4|=-(√2-√4)
ȘtergereObservam că numărul radical din 2 este mai mare decat radical din 1 si mai mic decat radical din 4. Radical din 4 este egal cu 2. Deci radical din 2 este mai mic decat 2, deci diferenta radical din 2 - 2 este o cantitate negativa. Modulul unei cantități negative este egal cu acea cantitate luată cu semn schimbat, adică minus. Astfel: modulul dat = -( radical din 2 - 2)= 2 - radical din 2.
RăspundețiȘtergere|3x-1|=|4x-3| asta cum se rezolva?
RăspundețiȘtergereAcest comentariu a fost eliminat de administratorul blogului.
ȘtergereBuna ziua ! Aveti o idee cum ar trebui facut in cazul |x|+|x+2|=3 ?
ȘtergereAcest comentariu a fost eliminat de autor.
ȘtergereAcest comentariu a fost eliminat de autor.
ȘtergereIn acest exercitiu sunt doua module. Pentru a rezolva ecuatia, trebuie sa explicitam modulele (sa aflam expresiile fara bare ale modulelor). Ca urmare:
Ștergere|x|={ x, dacă x>0
0, daca x=0
-x, dacă x<0
și al doilea modul:
|x+2| = { x+2, dacă x+2>0 => x>-2 =>
x aparține intervalului(-2, +inf);
0 dacă x = -2,
-(x+2), dacă x+2<0 => x<-2 =>
x aparține intervalului (-inf, -2).
Centralizăm pe axa numerelor reale, condițiile de mai sus și formele celor două module
-inf--------------- -2 ----------- 0 -----------> +inf
....... -x................ -x............. x
....... -x-2.............. x+2............ x+2
Din cele scrise mai sus, observăm că:
1) dacă x aparține intervalului (-inf,-2),
primul modul are expresia -x si
al doilea modul are expresia -x-2.
Ecuația, in acest caz, arată astfel:
-x-x-2=3 => -2x = 2+3 => -2x=5 => x = 5: (-2) = -2,5.
x= -2,5 este o soluție a ecuației deoarece aparține intervalului (-inf, -2) pentru care există această formă a ecuației.
2) Dacă x aparține intervalului închis [ -2, 0]
primul modul are forma -x , iar al doilea modul ia forma x+2
Ecuația arată astfel:
-x +x+2=3 => 2=3 => imposibil
Deci pentru acest interval ecuația nu are soluții.
3) In ultimul caz, dacă x >0 (x aparține intervalului 0, +inf),
primul modul are expresia x, iar al doilea modul are expresia x+2, iar, ecuația arată astfel:
x+x+2 = 3
2x = 3-2 =1 => x = 1/2 = 0,5. Această valoare este soluție a ecuației deoarece 0,5 aparține intervalului (0, +inf) .
La final, mulțimea soluțiilor ecuației o scriem astfel:
S = { -2,5 ; 0,5}
||x-3|-3|=5 cum se rezolva?
RăspundețiȘtergereAvem două cazuri:
Ștergeremodul (x-3) -3 = 5 sau modul (x-3) -3 = -5
Cazul 1: modul (x-3) = 3+5 = 8 => (x-3) = 8 sau (x-3)= -8
obținem o soluție x=3+8=11 și o a doua soluție x =3-8=-5.
Deci, la cazul 1 : x =11 sau x = -5.
Cazul 2: modul (x-3) = 3-5=-2. Un modul poate fi doar pozitiv (sau zero). Deci un modul = -2 este imposibil. În cazul 2 nu avem nici o soluție.
La final : x = -5 sau x = 11.
||x-3|-3|=5 cum se rezolva?
RăspundețiȘtergere|a|=|b|=>a=±b
RăspundețiȘtergereCazul 1: 3x-1=4x-3=>-1+3=4x-3x=>x=2
Cazul 2: 3x-1=-4x+3=>3x+4x=3+1=>7x=4=>x=4/7
Deci x=2 si x=4/7
Caz 1
RăspundețiȘtergere3x-1=4x-3 => 3x-4x=-3+1 => -x=-2 => x=2 (facem proba:|5|=|5|=>5=5;
Caz 2
3x-1=-(4x-3)=> 3x-1=-4x+3 => 3x+4x=1+3 => 7x=4 => x=4/7
Facem proba |5/7| =|-5/7| => 5/7=5/7; rezultă două soluții
X=2 si x=4/7
|x+3|=7 Cum se rezolva?
RăspundețiȘtergereVedeți rezolvarea de mai jos!
Ștergere|x+3|poate avea două expresii:
RăspundețiȘtergerea)
x+3 in cazul în care x+3>0, x>-3
Cu această expresie ecuația devine x+3=7, de unde rezulta x=4. Aceasta solutie este buna deoarece este mai mare decat -3 (din condiția modulului).
b)
-(x+3) daca x+3<0, x<-3
Cu această expresie a modulului, ecuația este:
-x-3=7
-x=7+3, -x=10, x=-10
Si aceasta solutie este buna deoarece este mai mica decat -3.
Ecuația are două solutii:
x=4 Si x=-10.
Cum se face |6-(-8)|
RăspundețiȘtergere6-(-8) = 6+8=14 (tinem cont ca semnul minus (-) in fata unei paranteze schimba toate semnele din paranteza. Deci -(-8) = +8 si rezultatul este +14, acesta este un numar pozitiv.
ȘtergereModulul unui numar pozitiv este egal cu acel numar pozitiv
|6-(-8)|= |14| = 14
/a-b+1/+/a+2b-3/=0. ??
RăspundețiȘtergereInteleg ca este vorba de o sumă a doua module care este egala cu zero. Stim ca modulul are intotdeauna valoare pozitivă sau zero. Rezultă că avem de adunat două valori > sau = cu zero. Logic nu putem obține rezultatul zero decat in cazul in care adunam zero cu zero! Deci cele doua expresii aflate în modul trebuie sa fie egale cu zero. Atunci avem: a-b+1=0 Si a+2b-3=0 două ecuații pe care le rezolvăm în sistem. Din prima ecuație rezultă a=b-1; din a doua rezultă a=-2b+3. Egalam cele doua expresii si obținem b-1=-2b+3;
RăspundețiȘtergereApoi b+2b=3+1; 3b=4; b=4/3. Iar a=b-1=4/3-1=4/3-3/3=1/3.
Solutie:a=1/3 si b=4/3.
Verificare:
|1/3-4/3+1|+|1/3+2×4/3-3|=|-3/3+1|+|1/3+8/3-3|=|-1+1|+|9/3-3|=|0|+|3-3|=0+0=0
|-11+9|=?
RăspundețiȘtergereMai intai facem calculul -11+9=-2, apoi |-2|=+2
ȘtergereModulul unei sume de numere este egal cu suma mudulelor numerelor respective?
RăspundețiȘtergereModulul unei sume de numere este 0 Si b<0, sau daca a<0 Si b>0;
Ștergere|a+b|=|a|+|b| daca a>0 Si b>0; sau daca a<0 Si b<0
Modulul unei sume de numere este mai mic sau egal cu suma modulelor celor două numere. |a+b|=|a|+|b| daca cele doua numere au același semn (amandoua pozitive sau amândouă negative);
RăspundețiȘtergere|a+b|<|a|+|b| daca cele doua numere au semne diferite a>0 Si b<0 sau a<0 Si b>0.
|6x-3|=45
RăspundețiȘtergereCazul 1. 6x-3=45 -> 6x=3+45=48-> x=48:6=8, x=8 este prima soluție.
ȘtergereCazul 2. 6x-3=-45 -> 6x=3-45=-42
X=-42:6=-7 a doua soluție.
Ecuația are două solutii: -7 Si 8.
Cum se face |a-3radical din 3|+|b-4radical din 3| mai mic sau egal cu 0?
RăspundețiȘtergereVedem ca sunt adunate două module. Știm că modulul intotdeauna este un număr pozitiv sau zero. Putem să adunăm două numere pozitive si sa obținem o sumă negativă? Nu! Este imposibil. Rezultă că doar cazul in care fiecare modul are valoarea zero este posibil sa adunam zero cu zero si obținem egalitatea cu zero.
RăspundețiȘtergereRezultă din această judecată ca fiecare modul trebuie sa fie egale cu zero. |a-3radical din 3|=0 deci a=3radical din 3 si |b-4radical din 4|=0 deci b =4radical din 3.
|2x-1|=0?? Nu înțeleg mie mi-a dat - 2
RăspundețiȘtergere2x-1=0, rzultă 2x=1 și x =1/2
ȘtergereModulul este egal cu zero atunci când expedia din modul este egala cu zero. Deci 2x-1=0, 2x=1, x= 1:2=1/2. Ne reamintim că proba la înmulțire se face prin împărțire!!!
RăspundețiȘtergereCum calculăm a=|6-8i|-|1+i radical din 3|???
RăspundețiȘtergereCum pot rezolva a=|6-8i|-|1 +i radical din 3|???
RăspundețiȘtergereIn exercitiu avem numere complexe.In general modulul unui număr complex de forma z= a+ib este modul de z = radical din (a pătrat + b pătrat). La noi primul nr. complex z1 are a = 6 și b = -8 și aplicând formula modulul lui z1 = radical din [6*6+(-8)*(-8)] = radical din 36+64 = radical din 100 = 10. Al doilea număr complex z2 are a=1 și b=radical din 3. Aplicând formula modulul lui z2 =radical din [1*1 + (radical din 3*radial din 3)]= radical din (1+3) = radical din 4 = 2. La final numarul a = modulul lui z1-modulul lui z2 = 10 - 2 = 8.
ȘtergereÎn exercițiu avem numere complexe(nivel liceu). Modulul unui număr complex a+ib= valoare pozitivă, = radical din (a la puterea 2 + b la puterea 2).
RăspundețiȘtergereModul (6-8i) = radical din (6 la 2 + 8 la 2)= radical din (36+64)= radical din 100 =10. La fel si la al doilea modul (1+3i)= radical din (1x1+3x3)=radical din (1+9)=radical din 10. Numărul a=10-radical din 10.
Cum calculam |2-1/4|+|1-3/2|+|2/3-4|??
RăspundețiȘtergereLuam fiecare modul si mai intai calculăm apoi rezolvam modulul:
Ștergere2-1/4=8/4-1/4=7/4>0. Este numar pozitiv. Modulul unui numar pozitiv este chiar acel numar.|7/4|=7/4.
Al doilea modul.
1-3/2=2/2-3/2=-1/2. Observam ca aceasta scadere ne da un numar negativ. Modulul unui numar negativ este egal cu numarul însuși luat fără semn.|-1/2|=1/2.
Al treilea modul:
2/3-4=2/3-12/3=-10/3.Observam ca in urma acestui calcul am obținut tot un numar negativ. Modulul lui este egal cu numarul însuși luat fără semn. |-10/3|=10/3.
Acum scriem exercitiul inlocuind modulele cu valorile obtinute:
7/4+1/2+10/4=7/4+2/4+10/4=
19/4.
Modul x+3 <sau egal 4
RăspundețiȘtergeremodul (x+3) < sau egal cu 4 se mai scrie
Ștergere-4 sau egal -7 (1)
x < sau egal +4-3, rezulta x < sau egal +1, (2)
Din relațiile (1) si (2) obținem: x apartine intervalului închis [-7, +1]. Atenție la cerința problemei! Dacă soluția se referă la numere reale, întregi sau naturale.
O intrebare :Cand in conditie scriesa afli parimetrul lui a daca solutia (x)este pozitiva,Atunci x>0 sau x> sau egal 0 .In carte raspunsul este un interval cu paranteze rotunde ,deci... este nu trebuie egal cu zero cu doar ca e mai mare Asta inseamna ca 0 nu este o solutie ...pozitiva?
RăspundețiȘtergeresolutia pozitiva este x>0 (strict). O nu este nici pozitiv, nici negativ.
ȘtergereModulul numarului minus radical din 7 este ....???
RăspundețiȘtergere- radical din 7 , este numar negative. Modulul lui este num[rul luat fara semn, adica radical din 7.
ȘtergereModulul numarului minus radical din 7 este ....???
RăspundețiȘtergereModulul unui număr negativ este egal cu numărul luat fără semn.
RăspundețiȘtergeremodul (-radical din 7) = radical din 7
Cum se rezolvă |10-radical din 2|
RăspundețiȘtergereModulul unui număr real - avem trei variante,
RăspundețiȘtergeredacă numărul este pozitiv, modulul este egal cu acel număr;
dacă numărul este egal cu zero, modulul este egal cu zero;
dacă numărul este negativ, modulul este egal cu -1 înmulțit cu acel număr (adică luăm numărul fără semn).
În acest exercițiu radical din 2 este aproximativ 1,41...si este mai mic decât 10. Când scădem din 10 acest 1,41 vom obține un număr (o diferență) pozitiv. Modulul acestui număr (dierența) pozitiv este egal cu acel număr. Deci:
modul de( 10-radical din 2) = 10-radical din 2.
(|-0,1|+|0,2|-|-0,3|):|-2019|
RăspundețiȘtergere-0,1 este numar negativ, modulul lui eeste 0,1 (adica numarul luat fara semn)
Ștergere-0,3 este tot numar negativ, modulul lui este 0,3
0,2 este numar pozitiv, modulul lui este 0,2 (adica ramane la fel, pozitiv).
-2019 este negativ, modulul lui este 2019.
In concluzie avem:
(0,1+0,2-0,3):2019=0:2019=0
0 impartit la orice numar diferit de ze zero = 0.
Cum se rezolva |sin x|
RăspundețiȘtergereFuncția sin x are valori pozitive atunci cand x apartine intervalului (0, Pi), are valori negative cand x apatine intervalului (Pi, 2Pi) si are valoarea zero pentru x =0, Pi, 2Pi, 3Pi...etc in general notam x= k Pi unde k apartine lui Z, multimea nr.intregi.
RăspundețiȘtergereHai sa generalizam ce am scris mai sus:
sin x este are valori pozitive , sau six x > 0 atunci cand x apartine intervalului (2kPi,(2k+1)Pi ) pentru orice nr k apartinand multimii numerelor reale. Vedem ca in cazul particular k=0 obtinem intervalul (0, Pi).
Pentru acest caz, modulul lui sin x |sin x| = sin x. Exact ca la |3|= 3.
In cazul al doilea , sin x ia valori negative atunci cand x apartine intervalului ( Pi, 2Pi) pe care il notam in general ca intervalul ((2k+1)Pi,(2k+2)Pi) pentru orice k apartinand multimii Z a numerelor intregi.
Modul de sin x, |sin x| = -sin x. Suntem obligati sa inmultim functia sin x cu (-1) si astfel schimbam semnul valorilor functiei din negativ in pozitiv.
In concluzie:
|sin x|= sin x, cand x€(2kPi, (2k+1)Pi),
=-sin x, cand x€((2k+1)Pi,(2k+2)Pi).
Si |x-7| = |x-8| cat face?
RăspundețiȘtergereVedeti raspunsul in comentariul din 14 febr.2021
ȘtergereSi |x-7| = |x-8| cat face
RăspundețiȘtergereLuam fiecare modul si il explicitam:
RăspundețiȘtergere|x-7|=x-7, daca x>7;
= 0, daca x=7;
=-x+7, daca x<7;
Si celalalt modul:
|x-8|= x-8, daca x>8;
=0, daca x=8;
=-x+8, daca x<8.
Vom lua pe rand toate cazurile, astfel:
Daca x<7, cele doua module vor avea expresiile: -x+7 si -x+8 si ecuatia arata astfel:
-x+7=-x+8, rezulta 7=8 ceea ce este imposibil, deci ecuatia nu are soluții.
Daca x=7sau x=8, de asemenea rezultatul este o impisibilitate.
Daca x>8, cele doua module iau expresiile x-7 si x-8, iar ecuatia arata astfel:
x-7=x-8, din care rezulta 7=8 , ceea ce este imposibil, deci ecuatia nu are solutii.
Mai ramane de studiat cazul in care 7<x<8, x apartine intervalului (7;8)
In acest caz primul modul are expresia x-7, iar al doilea modul are expresia -x+8.
In acest caz ecuația arata astfel:
x-7=-x+8
2x=15
x=15/2=7,5
Deci ecuatia are solutia unica x=7,5.
|x+2|>4
RăspundețiȘtergereCum se calculează?
Incepem prin a explicita modulul |x+2|. Ca urmare acesta poate avea forma
Ștergere1) x+2 in cazul in care x+2 este o cantitate pozitiva, adica x+2>0, ceea ce inseamna x>-2 sau x apartine intervalului (-2, +infinit);
Sau forma
2) -(x+2) in cazul in care x+2 este o cantitate negativa, adica x+2<0 sau x apartine intervalului (-infinit, -2).
Acum vom rezolva inecuatia pentru cele doua cazuri. Astfel;
1) daca x apartine intervalului (-2, +inf), inecuatia arata astfel:
x+2>4. Rezolvam trecand pe 2 in partea dreapta cu semn schimbat:
x>4-2, x>2, x apartine intervalului (2, +inf). Acest interval este solutie a inecuatiei deoarece este inclus in conditia (-2, +inf).
In cazul al doilea:
2) daca x apartine intervalului (-inf, -2), modulul ia cea de.a doua expresie -(x+2) si inecuatia arata astfel:
-(x+2) >4
-x-2>4
-×>2+4
-x>6 inmultim cu (-1) inecuatia si vom schimba toate semnele, inclusiv semnul inecuatiei,
Rezulta:
x<-6
soluția x apartine (-inf, -6), interval care este inclus in conditia (-inf, -2).
La final reunim cele doua solutii obtinute din cele doua cazuri si scriem solutia generala a inecuatiei:
x apatine (-inf, -6) reunit cu (2, +inf).
Va rog ...sunt cl 9 ...modul de 2x+3/x-3 mai mare decat 5 ( la capitolul functia de gradul 1 )
RăspundețiȘtergereIn acest exercitiu avem modulul unei fractii care este mai mare decat 5. In primul rand notam ca x poate fi un numar real cu exceptia lui 3, deoarece la 3 numitorul devine zero si in fractie s.ar face impartire la zero, ceea ce nu este permis. Deci x apartie multimii R \ {3}.
ȘtergereContinuam:
Fractia poate avea valori pozitive mai mari decat 5 sau valori negative mai mici decat -5. Pentru ambele cazuri modulul devine mai mare ca 5.
Aceasta inecuatie o putem scrie intr.un sistem de inecuatii in care nu mai avem modul. Astfel:
Sistem: se va deschide o acolada in care se pun inecuatiile:
(2x+3)/(x-3) > 5 si
(2x+3)/(x-3) < -5 .
Vom rezolva pe rand inecuatiile si la sfarsit solutiile le vom reuni intr.o solutie finala.
1)
(2x+3)/(x-3) > 5 ->
[(2x+3)/(x-3)]-5>0 ->
[2x+3-5(x-3)]/(x-3)>0 ->
(2x+3-5x+15)/(x-3)>0 ->
(-3x+18)/(x-3)>0
In aceasta fractie avem functii de gradul 1 la numarator si la numitor.
Numaratorul devine zero atunci cand -3x+18=0 -3x=-18 x= (-18)/(-3)=6
Numitorul devine zero la 3 si stim ca aceasta valoare trebuie inlaturata.
Vom completa tabelul de semn
X |-infinit 3 6 +infinit
‐---------------------------
-3x+18| ++++++++0---------
X-3 | ----|++++++++++++++
Fractia| ---|++++0---------
In dreptul lui 6 punem zero
Semnele le punem dupa regula "in stanga semnul contrar coeficientului lui x".
Cum x are coeficientul -3, deci negativ, punem semnul +
In dreapta "zeroului" punem semnul coeficientului lui x.
La x-3, la valoarea 3 vom pune zerolul dar il desenam cu o bară, pentru a avea grija sa scoatem aceasta valoare. Punem semnele: in stanga barei, aceeasi regula semn contrar coeficientului lui x. Deoarece in expresia x-3, x are coeficient +1 in stanga barei punem minus si plus in dreapta.
Apou trecem in tabel si fractia unde vom imparti semnele din tabel si coboram bara de la 3 si zeroul de la 6.
Observam ca fractia are valori strict pozitive pentru x >3 si x<6.
Solutia x apartine i intervalului (3; 6)
2.
A doua inecuatie:
(2x+3)/(x-3)+5<0
Ștergere[(2x+3)+5(x-3)]/(x-3)<0
(2x+3+5x-15)/(x-3)<0
(7x-12)/(x-3)<0
Numaratorul devine zero dacs
7x-12 =0 x=12/7 = aprox.1,7
Numitorul devine zero la 3.
Completam tabelul de semn:
X |-inf 12/7 3 +inf
7x-12|-------0 ++++++++++++
X-3 |-------------|+++++++
Fract|+++++++0-----|+++++++
Observam ca fractia are semnul negativ pentru x aflat intre 12/7 si 3
Deci x apartine (12/7;3)
Luam impreuna, reunim, cele doua solutii si scriem solutia generala:
X aparține intervalului
(12/7, 6)\{3}.
Deoarece nu se afiseaza corect tabelul, aveti grija ca 3 si bara sa fie pe aceeasi verticala, 12/7 si 6 cu zeroul corespunzator scris exact sub acestea.
ȘtergereCum s-ar rezolva |3x-12|?
RăspundețiȘtergere|1-x|va rog
RăspundețiȘtergerePentru rezolvare: va rog să citiți explicațiile de la comentariile de mai sus. Exercițiul cu |x+3| este asemenator.
ȘtergerePentru rezolvare, va rog să citiți explicațiile de la |x+3|. Se procedează la fel
RăspundețiȘtergere