EVALUAREA NAȚIONALĂ PENTRU ABSOLVENȚII CLASEI A VIII-a /model / rezolvare și barem Subiectul al II-lea

EVALUAREA NAȚIONALĂ PENTRU ABSOLVENȚII CLASEI A VIII-a  /model  / rezolvare și barem

Anul școlar 2014 – 2015  

Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

Timpul efectiv de lucru este de 2 ore (pentru cele 3 subiecte)

Subiectul al II-lea  - (30 puncte) Pe foaia de examen scrieți rezolvările complete  

 

5p 5p 5p 5p 5p    5p

1.  Desenați, pe foaia de examen, un paralelipiped dreptunghic ABCDEF. Soluție: Se desenează paralelipipedul: prisma dreapta cu baza dreptunghi (4 puncte) și apoi se notează ABCDEFGH (1 punct) 2. Calculați media aritmetică a numerelor reale                                                                                           Rezolvare:  media aritmetică se obține prin împărțirea sumei numerelor la numărul total de numere. Formula de calcul a mediei aritmetice: Ma = (x + y) : 2  Calculăm x (2 puncte) Apoi calculăm media aritmetică:        (3 puncte) 3. Un autoturism a parcurs un traseu în două zile. În prima zi autoturismul a parcurs 30% din lungimea traseului, iar în a doua zi autoturismul a parcurs restul de 350 km. Calculați lungimea de întregului traseu. Rezolvare: Notăm cu x lungimea întregului traseu, deoarece nu se cunoaște. În prima zi a parcurs 30% din întregul traseu. Această informație o vom nota:   (2 puncte) În cea de a doua zi a parcurs restul de 350 km, deci putem scrie întregul drum parcurs astfel:  (3 puncte) În ecuație am adus la același numitor, care este 10 (se amplifică cu 10 fiecare termen care nu are numitor). 4. Se consideră funcția f: R ̶> R, f(x) = ax + 3, unde a este un număr real. a) Determinați numărul real a, știind că f(-3) = 0. b) Pentru a = 1, arătați că triunghiul OAB este isoscel, unde A și B sunt punctele de intersecție a graficului funcției f cu axele Ox, respectiv Oy ale sistemului de coordonate xOy. Rezolvare: a)   Condiția f(-3) = 0 înseamnă că atunci când x ia valoarea -3, funcția are valoarea 0. În expresia funcției înlocuim x cu -3 și obținem: f(-3) = (-3)·a + 3. 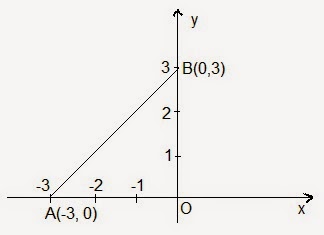(2 puncte) Această expresie o introducem în condiția dată de problemă f(-3) =0,  ceea ce conduce la  -3a +3 = 0 sau -3a = -3, din care se obține   a = (-3) : (-3) = 1  , a = 1  (3 puncte) b)   Când a = 1 expresia funcției noastre este f(x) = x + 3. Cunoaștem că punctele de intersecție cu axele de coordonate se obțin astfel: punctul de intersecție cu axa Ox este un punct care are ordonata egală cu zero, ordonata este y = f(x) = 0 rezultă x+3 = 0 Din care x = -3 deci punctul de coordonate (-3, 0) este punctul de intersecție cu axa Ox. (2 puncte) Punctul de intersecție cu axa Oy are abscisa egală cu 0 sau x = 0. Rezultă f(0) = 0 + 3 = 3. Punctul de intersecție cu axa Oy are coordonatele (0, 3) . Triungiul OAB are latura OA egală cu 3 cm (în modul) și latura OB egală cu 3 cm, deci este isoscel. (3 puncte) 5. Se consideră expresia. Unde x este un număr real, x ≠ 0 și x ≠ 1 Determinați numărul real m, m ≠ 0 și m ≠ 1, știind că E(m) = 5. Rezolvare: Aducem la o formă mai simplă expresia E(x). Condițiile de existență pentru expresie sunt deja date de problemă pentru a se evita împărțirea la zero (numitorii sau împărțitorii să nu fie zero) de aici avem x diferit de 0 și de 1. Folosim metodele de descopunere în factori: scoterea de factor comun și formula diferenței de pătrate a2 – b2 = (a-b) (a+b). Obținem:   Pentru a obține E(m) = 5 înlocuim necunoscuta x cu acest număr real m și obținem: E(m) = m + 3 și dăm valoarea 5 pentru această expresie. Obținem ecuația:  m + 3 = 5 din care rezultă m = 5 – 3 = 2                      (1 punct) Soluția m = 2.