Problema geometrie clasa a VIII-a / Concursul Lumina Math 2014
În trapezul ABCD, BC⊥AB, BC⊥CD și AC⊥BD. Știind că


În primul rând desenăm figura. Pentru aceasta ținem cont de datele problemei BC⊥AB, BC⊥CD , din care rezultă că laturile paralele ale trapezului sunt AB și CD ( AB ∥CD). De asemenea, avem grijă să facem o figură în care diagonalele AC și BD să fie perpendiculare.
Deoarece diagonalele sunt perpendiculare și se intersectează în punctul notat cu O, putem nota BO ⊥AC și DO⊥AC . Astfel scoatem în evidență faptul că BO și DO sunt înălțimi în Δ ABC și Δ DAC.
Aria trapezului ABCD se poate scrie ca suma ariilor triunghiurilor ABC și DAC.
Cunoaștem acestă
formulă : Aria unui patrulater care are diagonalele perpendiculare este egală
cu jumătate din produsul diagonalelor.
Pe de altă parte aria trapezului este egală cu produsul dintre semi-suma bazelor și înălțimea trapezului.
Pe de altă parte aria trapezului este egală cu produsul dintre semi-suma bazelor și înălțimea trapezului.
Egalând cele două
relații obținem o primă ecuație:
Observăm din figură
că avem cunoscute două laturi ale trapezului și două sunt necunoscute. Notăm cu
x latura BC și cu y latura CD.
Pentru a exprima
diagonalele ne folosim de teorema lui Pitagora pe care o aplicăm în
triunghiurile ABC și BCD. Astfel avem:
Înlocuim în aceste
relații valorile și notațiile din figură:
Înlocuim expresiile
obținute pentru diagonale le înlocuim în relația 3 și obținem:
Aducem această
relație la o formă mai simplă prin ridicare la pătrat (atât membrul stâng cât
și cel drept din ecuație).
Am obținut o primă
ecuație între x și y, cele două necunoscute.
Pentru o a doua
relație, construim perpendiculara din A pe latura CD și notăm punctul M. ABCM
este un dreptunghi și CM este congruent cu AB. Rezultă că DM este egal cu:

În triunghiul
dreptunghic ADM aplicăm teorema lui Pitagora și obținem:
Facem înlocuirile cu
valorile și notațiile corespunzătoare:
Ținem cont de
relația 6 și înlocuim x cu expresia în
y. Rezultă:

În această relație formăm un binom la pătrat prin următoarele operații ajutătoare:
- Pentru a forma termenul din mijloc al formulei binomului la pătrat: înmulțim termenul care conține y cu un 2 și împărțim cu 2;
- Recunoaștem în acest termen din mijloc forma celui de-al doilea termen al binomului
- Pentru a avea și cel de-al doilea pătrat perfect din formulă adunăm și scădem valoarea pătratului acestui al doilea termen al binomului care lipsește. Avem astfel:
- Pentru a forma termenul din mijloc al formulei binomului la pătrat: înmulțim termenul care conține y cu un 2 și împărțim cu 2;
- Recunoaștem în acest termen din mijloc forma celui de-al doilea termen al binomului
- Pentru a avea și cel de-al doilea pătrat perfect din formulă adunăm și scădem valoarea pătratului acestui al doilea termen al binomului care lipsește. Avem astfel:

Valoarea
negativă este imposibilă deoarece segmentul ia doar valori pozitive.
Deci 
Și pe x îl obținem din relația 6
Soluția problemei: varianta E








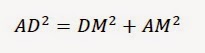



Niciun comentariu:
Trimiteți un comentariu