și AB = 6 dm. Punctul M este mijlocul laturii AD.
A)
Arătați că VM = 6 dm.
B)
Calculați câte grame de vopsea sunt necesare
pentru vopsirea suprafeței totale a piramidei știind că pentru vopsirea unei
suprafețe de un decimetru pătrat se folosesc 30g de vopsea.
Demonstrați că sinusul unghiului dintre planul (VAD)
și (VBC) este egal cu
Rezolvare:
A)
Deoarece VABCD piramidă patrulateră regulată
rezultă că baza piramidei este un pătrat și toate muchiile sunt congruente
între ele. Putem scrie: AB = BC = CD = DA = 6 dm și
Rezultă că fețe laterale sunt triunghiuri isoscele. În
triunghiul VAD isoscel (VA = VD) avem M mijlocul laturii AD. Rezultă că VM este
mediană în triunghiul VAD. Cunoaștem că în triunghiul isoscel, mediana dusă de
la vârful din care pleacă și laturile congruente ale triunghiului este și
mediatoare, înălțime și bisectoare. Deci, putem scrie VM ^ AD. În triunghiul
dreptunghic VAM cunoaștem VA ipotenuza și AM cateta, care este jumătate din AD,
AM = 3 dm. Aplicăm teorema lui Pitagora și calculăm VM:
VM2 = AV 2- AM2= 32∙5
– 32= 45 – 9 = 36 = 62. Rezultă VM = 6 dm.
B)
Pentru a calcula cantitatea de vopsea avem
nevoie să cunoaștem suprafața totală a piramidei. Suprafața totală are o arie
totală egală cu: Atot= Abazei + Alat.
Aria bazei = aria pătratului ABCD = AB2= 62=36
dm2.
Aria laterală = (Perimetrul bazei ∙ apotema piramidei)/2 =
4AB∙VM/2 = 4∙6∙6/2= 72dm2.
Aria totală a piramidei = Aria bazei + aria laterală = 36 +
72 = 108 dm2.
Cantitatea de vopsea folosită pentru vopsirea suprafeței
totale = 108 dm2 ∙ 30 g/ dm2= 3240 g vopsea = 3,24 kg
vopsea.
C)
Unghiul dintre planele VAD și VBC, așa cum
cunoaștem din definiție, este determinat de două drepte (situate una într-un
plan și cealaltă în celălalt plan) perpendiculare pe dreapta de intersecție a
celor două plane. Deoarece în planele
VAD și VBC avem dreptele AD și BC care sunt laturile opuse ale pătratului de la
bază și sunt paralele între ele, rezultă că planele VAD și VBC se vor
intersecta după o dreaptă g paralelă cu AD și BC și care trece prin punctul V,
comun celor două plane. Deoarece în planul VAD avem VM perpendiculară pe AD,
atunci VM este perpendiculară și pe dreapta g (paralelă la AD). La fel, în
planul VBC avem VN perpendiculară pe BC și totodată perpendiculară pe dreapta
g. Deci unghiul dintre planele VAD și VBC este unghiul dintre VM și VN :
unghiul MVN.
Tot ce am povestit vom scrie matematic
astfel:
În triunghiul VMN avem MN = AB = 6 dm, VM = VN = 6 dm
(deoarece triunghiurile fețelor laterale sunt congruente între ele și
înălțimile lor sunt congruente între ele). Rezultă că triunghiul VMN este
echilateral și are toate unghiurile cu măsura de 60 grade.
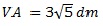






Niciun comentariu:
Trimiteți un comentariu