Fie triunghiul ABC, în care AB<AC. Fie punctele D şi E

a) demonstraţi că triunghiul ABF este isoscel;
b) demonstraţi că
Demonstrație:

Pentru a construi figura ne folosim de următoarele notaţii
Observăm că triunghiurile AMB şi AMF sunt congruente deoarece:
din această congruenţă (cazul de congruență catetă unghi) rezultă că şi celelalte elemente ale celor două triunghiuri sunt congruente:
Pentru punctul b) observăm că triunghiurile AND şi ANG sunt congruente (cazul catetă unghi) deoarece:
Pentru a exprima măsura segmentului FG umărim să calculăm cele două segmente care adunate formează segmentul FG= FC + CG. În acest scop ne folosim de notațiile următoare:
Observăm că relația AD =AG de mai sus pe AD îl scriem ca sumă de segmente AB și BD, iar CF ca diferență de segmente AC și AF. AE este egal cu suma dintre AC = b și CE = x
Prin urmare, segmentul EG îl exprimăm ca diferență de segmente AE-AG și calculăm înlocuind expresiile pentru fiecare segment:
Rezultă că EG și CF sunt segmente egale (au aceeași măsură). Acum putem să calculăm valoarea segmentului GC ca diferență dintre AG și AC:
În final calculăm valoarea măsurii segmentului FG ca sumă a măsurilor segmentelor FC și CG:
Deoarece am obținut aceeași măsură pentru cele două segmente FG=x și CE =x rezultă că cele două segmente sunt congruente.

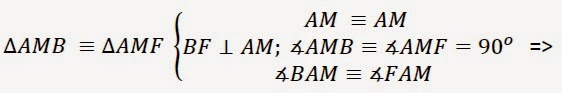





Niciun comentariu:
Trimiteți un comentariu